第三讲:一元函数微分学的概念
第三讲:一元函数微分学的概念
1. 导数的定义
\begin{array}{l}
\Delta y=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right) \quad \lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} \text { 存在, 则称 } f(x) \text { 在 } x_{0} \text { 处可导 } \\
\text { 记 } f^{\prime}\left(x_{0}\right)=\lim _{\Delta x \rightarrow 0 } \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}\left(=\left.\frac{d y}{d x}\right|_{x=x_{0}}\right )
\end{array}
单侧导数
- 左导数:
\lim_{\Delta x \to 0^-} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = f'_-(x_0)
- 右导数:
\lim_{\Delta x \to 0^+} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = f'_+(x_0)
左右导数存在且相等 \Leftrightarrow 导数存在
f'(x_0) \text{ 存在 } \Leftrightarrow f'_+(x_0) = f'_-(x_0) = A
切线与导数关系
- 有切线不一定有导数
- 有导数一点有切线
有导数一定有切线
\begin{array}{l}
\left\{\begin{array}{l}
f^{\prime}\left(x_{0}\right) \neq 0 \\
f\left(x_{0}\right) \text { 可导 }
\end{array} \Rightarrow|f(x)| \text { 在 } x_{0}\right. \text { 可导 } \\
\left\{\begin{array}{l}
f\left(x_{0}\right)=0 \\
f^{\prime}\left(x_{0}\right) \neq 0 \\
f(x) \text { 在 } x_{0} \text{可导}
\end{array} \Rightarrow|f(x)| \text { 在 } x_{0}\right. \text { 不可导 }
\end{array}
2. 导数的几何意义
曲线 y = f(x) 在点 x_0 处的导数值 f'(x_0) 就是曲线 y = f(x) 在 (x_0, y_0) 处切线的斜率。
切线存在,导数不一定存在(铅垂)
3. 高阶导数
- f(x) 在 x = x_0 处可导。
- 若 f'(x_0) = 0 且 f''(x_0) > 0,则 f(x) 在 x_0 处取极小值。
- 若 f'(x_0) = 0 且 f''(x_0) < 0,则 f(x) 在 x_0 处取极大值。
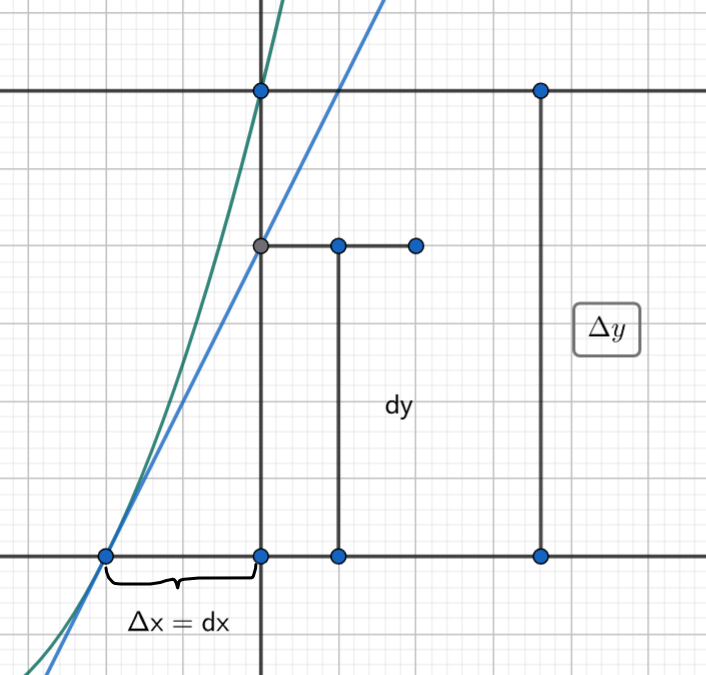
4. 微分的概念
设函数 y = f(x) 在点 x_0 的某邻域内有定义,且 x_0 + \Delta x 在该邻域内。
对于函数增量 \Delta y = f(x_0 + \Delta x) - f(x_0),若存在与 \Delta x 无关的常数 A,使得
\Delta y = A \Delta x + o(\Delta x),
称 f(x) 在 x_0 处可微。其中 A \Delta x 称为线性主部,也叫做 f(x) 在点 x_0 处的微分。
记
dy|_{x=x_0} = A \Delta x \quad \text{或} \quad dy|_{x=x_0} = f'(x_0) dx
于是
\Delta y = dy + o(\Delta x).
可微的判别
\Delta y = f(x_0 + \Delta x) - f(x_0)
A \Delta x = f'(x_0) \Delta x
\lim_{\Delta x \to 0} \frac{\Delta y - A \Delta x}{\Delta x} \Leftrightarrow \Delta y = A \Delta x + o(\Delta x)
其中\lim_{\Delta x \to 0} \frac{\Delta y - A \Delta x}{\Delta x}极限值为 0。
第三讲:一元函数微分学的概念
http://localhost:8090//archives/di-san-jiang-yi-yuan-han-shu-wei-fen-xue-de-gai-nian