第一讲：函数极限与连续

1. 函数的概念

• ​y, x 自变量、因变量
• ​x \in D，有一个确定的值与 ​y 对应（单值函数）
• 多值函数：
  y = f(x)

判断：数形结合

铅锤直线法：

若任一条铅垂直线与 ​f(x) 至多一个交点，则 ​f(x) 为单值函数。

2. 反函数（符合铅直画线法）

（1）严格单调函数必有反函数（充分条件）

（2）​f(x) 与 ​f^{-1}(y) 在同一坐标系中，图像完全重合。

• 只有把 ​y = f(x) 的反函数 ​x = f^{-1}(y) 写成 ​y = f^{-1}(x) 后，才关于 ​y = x 对称。

判断是否有反函数：水平画线法

---

奇偶性

奇函数

• 反双曲正弦函数：

  y = \ln(\sqrt{x^2 + 1} + x) = -\ln(\sqrt{x^2 + 1} - x)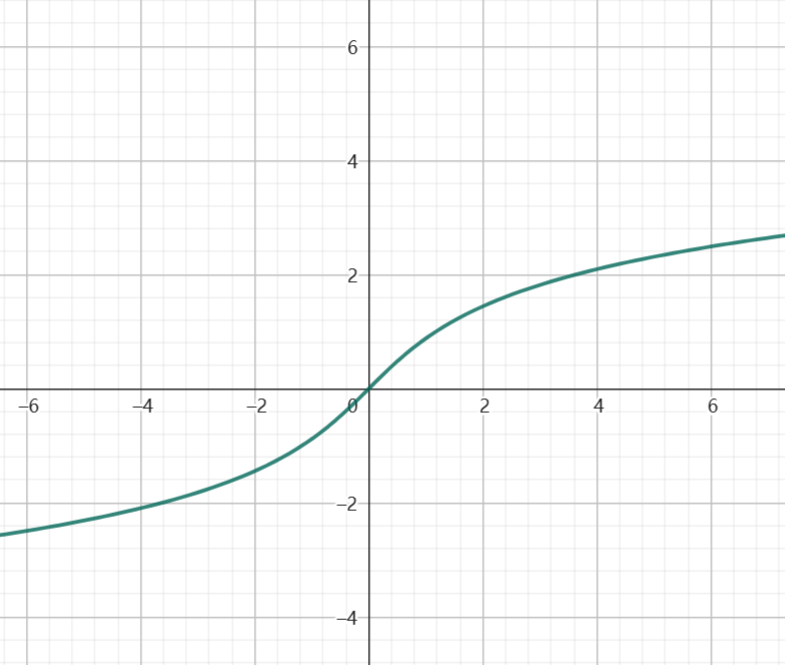

  

• 双曲正弦函数：

  y = \frac{e^x - e^{-x}}{2}

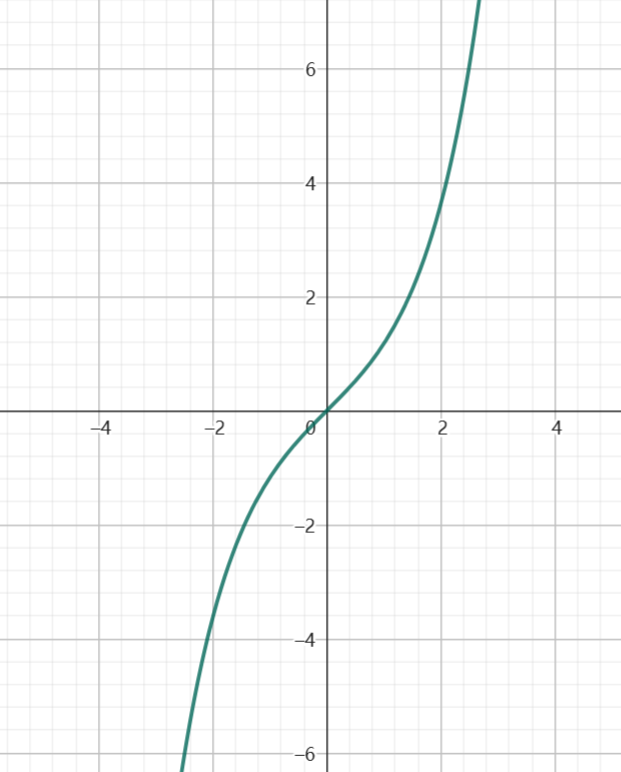
偶函数

• 双曲余弦函数：

  y = \frac{1}{2}(e^x + e^{-x})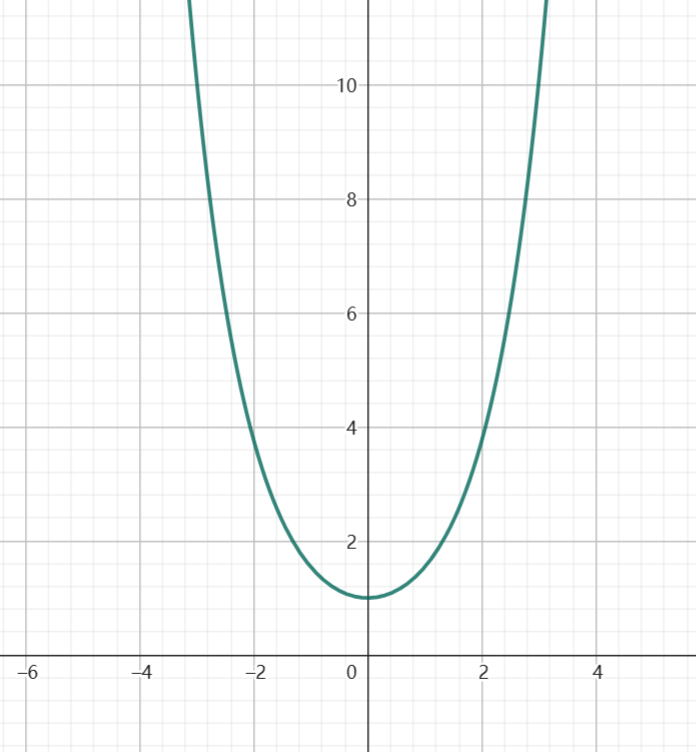

  

• 悬链线：

  y = \frac{1}{2}(e^{\frac{x}{a}} + e^{-\frac{x}{a}})

---

公式总结

1. \lim_{x \to 0} \ln(x + \sqrt{x^2 + 1}) \sim x
2. \int \frac{1}{\sqrt{1 + x^2}} \, dx = \ln(x + \sqrt{1 + x^2}) + C
3. \int_{-a}^{a} \ln(x + \sqrt{1 + x^2}) \, dx = 0

3. 复合函数

• ​y = f(u) 定义域 ​D，​u = g(x) 在 ​D 上有定义，且 ​g(x) \subset D，则称 ​y = f[g(x)] (x \in D) 为复合函数。
• 和 ​y = f(u) 构成的复合函数
• 定义域为 ​D，​u 称为中间变量。

---

4. 隐函数

设 ​F(x, y) = 0，若 ​x 取某区间内的任一值时，总有满足该方程的唯一值 ​y 存在，则称方程 ​F(x, y) = 0 在上述区间内确定了一个隐函数 ​y = y(x)。

---

5. 函数的四种特性

5.1 有界性

• ​f(x) 定义域 ​D，数集 ​I \subset D。若 ​\exists M > 0，​\forall x \in I，有 ​|f(x)| \leq M，则 ​f(x) 在 ​I 上有界；否则不存在，则 ​f(x) 在 ​I 上无界。
• 从解析上看，如果找到某个正数 ​M，使得 ​|f(x)| \leq M，则 ​f(x) 在 ​I 上有界。

5.2 单调性

• ​f(x) 定义域 ​D，区间 ​I \subset D。若任意两点 ​x_1, x_2 \in I，​x_1 < x_2，​f(x_1) < f(x_2)，则 ​f(x) 在 ​I 上严格单调递增。

5.3 奇偶性

• ​f(x) = f(-x)：偶函数
• ​f(x) = -f(-x)：奇函数
• 定义域关于原点对称。
• ​u = \frac{1}{2}[f(x) + f(-x)]：偶函数部分
• ​v = \frac{1}{2}[f(x) - f(-x)]：奇函数部分
• ​f(x) = u(x) + v(x)：任一个函数可以写成一个奇函数和偶函数的和。
• ​f(x) = \psi (x)：内偶则偶，内奇则奇。
• ​ f(x) 奇 \Rightarrow {f}'(x)偶\Rightarrow {f}''(x)奇。若函数可导，求导一次，奇偶性变化一次
• ​ f(x) 奇(偶) \Rightarrow \int_{0}^{x}f(t)\,dt偶(奇)
• 若任意​f(x+y)=f(x)+f(y)，则​f(X)是奇函数

---

5.4 周期性

• 若 ​\forall x \in D，​x + T \in D，且 ​f(x + T) = f(x)，则称 ​f(x) 是周期函数，周期为 ​T。

  • ​g(x)周期函数，​f(g(x))也是周期函数，如​f(x)={e}^{\sin x}

• 若 ​f(x) 是周期函数，可导，其导数也是周期函数，周期也为 ​T。

• 若 ​f(x) 是周期函数，则 ​\int_{0}^{T} f(x) \, dx = 0，则​\int_{0}^{X} f(t) \, dt以​T为周期

• 若 ​f(x) 是周期函数，则 ​f(ax + b) 是周期函数，则其周期为 ​\frac{T}{|a|}。

---

6. 基本初等函数

常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数

• ​y = A
• ​y = x^m
• ​y = a^x
• ​y = \log_a x

几个方便计算的方法

三角函数

• ​\arcsin x

  

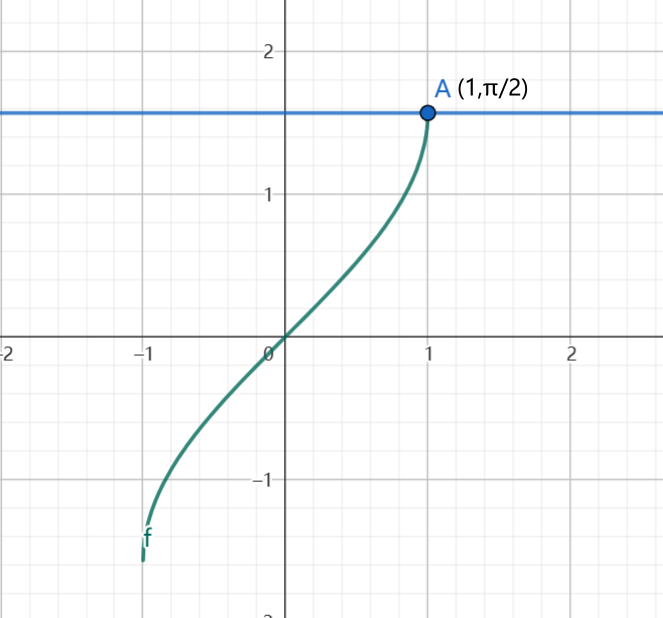
• ​\arccos x

  

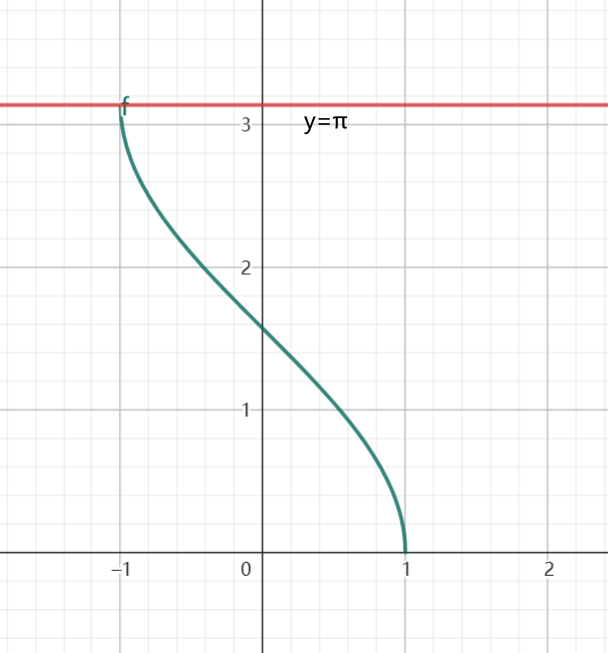
• ​\arctan x

  

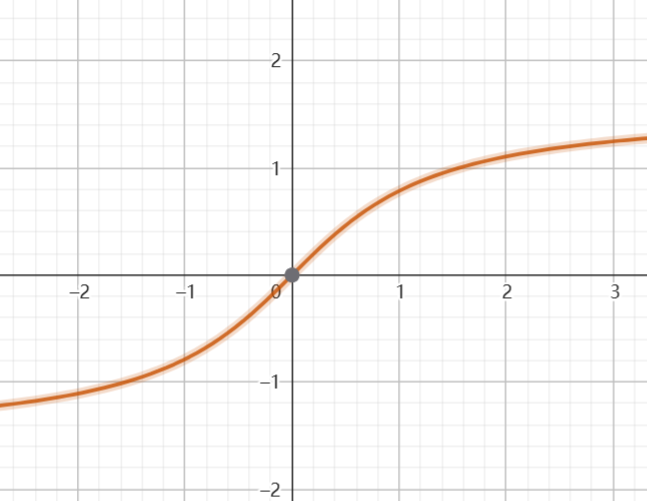
• ​\operatorname{arccot} x

---

7. 分段函数

---

8.邻域

定义

• ​ U(x_0, \delta) = \{ x \mid x_0 - \delta < x < x_0 + \delta \} = \{ x \mid |x - x_0| < \delta \}
  • ​\delta: 某一个正数

去心邻域

• ​ U^*(x_0, \delta) = \{ x \mid 0 < |x - x_0| < \delta \}

左邻域和右邻域

• 左邻域：​ U^-(x_0, \delta)
• 右邻域：​ U^+(x_0, \delta)

---

9.极限的定义

函数极限的定义

1. 若函数 ​ f(x) 在 ​ x_0 的某一个去心邻域内有定义，且存在常数 ​ A ，对于给定的任意 ​ \varepsilon > 0 ，总存在正数 ​ \delta ，使得当 ​ 0 < |x - x_0| < \delta 时，​ f(x) 都满足不等式 ​ |f(x) - A| < \varepsilon ，则称 ​ A 为 ​ f(x) 当 ​ x \to x_0 时的极限。

   • 记作：
     \lim_{x \to x_0} f(x) = A \quad \text{或} \quad f(x) \to A \ (x \to x_0)

2. 对于任意 ​ \varepsilon > 0 ，存在 ​ \delta > 0 ，当 ​ 0 < |x - x_0| < \delta 时，有 ​ |f(x) - A| < \varepsilon 。

---

10.超实数

实数与超实数

• 实数 ​\mathbb{R} → 超实数 ​\mathbb{R}^*
• 确界性：无穷小无法在数轴上表示。

超实数的定义

• 以 ​ x_0 为“核”的标准超实数：
  x = \text{std}(x_0) + \underbrace{x - \text{std}(x)}_{\text{无穷小}}

超实数的性质

1. 无穷小：

   • 在实数中，对于任意大的自然数 ​ n ，若 ​ |x| < \frac{1}{n} ，则 ​ x = 0 。
   • 在超实数中，对于任意大的自然数 ​ n ，若 ​ |x^*| < \frac{1}{n} ，且 ​ x^* \neq 0 ，则 ​ x^* 为非零无穷小。

2. 无穷大：

   • 设 ​ x 为任一实数，​ x + x^* 为有限超实数，​ k \cdot x^* 为无穷大（无限大）。

极限的运算

• 设 ​ \lim_{x \to x_0} f(x) = A ，​ \lim_{x \to x_0} g(x) = B 。

  • 加法：

    \lim_{x \to x_0} (f(x) + g(x)) = A + B \text{ 若有不存在，则不成立}

  • 其他运算类似。

---

11. 唯一性

如果 ​\lim_{x \to x_0} f(x) 存在，那么极限唯一。

即：

12. 局部有界性

• 如果：​\lim_{x \to x_0} f(x) = A，则存在正常数 ​M 和 ​\delta，使得当 ​0 < |x - x_0| < \delta，有 ​|f(x)| \leq M
• ​f(x)连续且​\lim_{x \to \infty} f(x)存在，则​f(x)有界，反之不成立
• 闭区间连续必有界

13. 局部保号性

若 ​f(x) \to A (x \to x_0) 且 ​A > 0（或 ​A < 0），那么存在邻域 ​\delta > 0，使得当 ​0 < |x - x_0| < \delta 时，有 ​f(x) > 0（或 ​f(x) < 0）

若在 ​x_0 某去心邻域内 ​f(x) \geq 0，且 ​\lim_{x \to x_0} f(x) = A，则 ​A \geq 0（或 ​A \leq 0）

14. 无穷小的定义

• 当 ​x \to x_0（或 ​x \to \infty）时，函数 ​f(x) 极限为零，则称函数 ​f(x) 当 ​x \to x_0（或 ​x \to \infty）时的无穷小。
  记 ​\lim_{x \to x_0} f(x) = 0
• 0 是唯一的常数的无穷小，在能化简的条件下，0 是最高阶无穷小。
• 无穷小（除 0）是一个趋于 0 的变量。
• 有限个无穷小的和为无穷小。
• 有界函数与无穷小乘积是无穷小。
• 有限个无穷小乘积为无穷小。

15. 无穷小的比较

不是任意两个无穷小都可以比较的，如 ​\sin \frac{1}{x} 与 ​x^2。

16. 极限的四则运算

若 ​\lim_{x \to x_0} f(x) = A，​\lim_{x \to x_0} g(x) = B，那么极限的加减乘除分别等于加减乘除的极限。

7. 洛必达法则

18. 泰勒公式

19. 无穷小的运算

20. 未定式计算

1. 化简先行
2. 判断类型（运算类型）
3. 选择方法

21. 夹逼准则

22. 连续的定义

设 ​f(x) 在点 ​x_0 的某个邻域内有定义，且有 ​\lim_{x \to x_0} f(x) = f(x_0)，则称 ​f(x) 在点 ​x_0 处连续。

​f(x)，​g(x) 在 ​x_0 处连续，则加减乘除也连续 (​g(x) \neq 0)

复合函数也连续，
反函数也连续，

若 ​f(x_0) 在 ​x_0 处连续，且 ​f(x_0) > 0，则 ​x_0 的邻域内，​f(x) > 0

23. 间断点的定义

第一类间断点（共两种）

1. 可去间断点（可补间断点）

2. 跳跃间断点

第二类间断点

1. 无穷间断点

​x_0 左右两侧至少有一个 ​\infty

2. 振荡间断点

若 ​f(x_0) 振荡不存在。如 ​x_0 = 0，​f(x) = \sin \frac{1}{x}