第五讲:一元函数
第五讲:一元函数
1. 极值的定义
对于函数 f(x) ,在 x_0 的某个邻域,在该邻域内任一点 x ,均有:
f(x) \leq f(x_0) \quad (\text{或 } f(x) \geq f(x_0))
则称 x_0 为 f(x_0) 的极大(小)值点。
端点不讨论极值、间断点
2. 单调性的判别
y = f(x) 在 [a, b] 上连续,在 (a, b) 可导。
如果在 (a, b) 内 f'(x) > 0 ,且等号在有限个点处成立,则函数 y = f(x) 在 [a, b] 上严格单调递增。
3. 一阶导点是极值点的必要条件
设 f(x) 在 x = x_0 处可导,且在点 x_0 处取极值,则必有: f'(x_0) = 0
4. 判别极值的第一充分条件
设 f(x) 在 x = x_0 处连续,且在 x_0 的某去心邻域 U(x_0, \delta) 内可导。
- 若 x \in (x_0 - \delta, x_0) 时, f'(x) > 0 ,而 x \in (x_0, x_0 + \delta) 时, f'(x) < 0 ,则 f(x) 在 x = x_0 处取极大值。
- 若 x \in (x_0 - \delta, x_0) 时, f'(x) < 0 ,而 x \in (x_0, x_0 + \delta) 时, f'(x) > 0 ,则 f(x) 在 x = x_0 处取极小值。
- 若 f'(x) 不变号,则不是极值点。
- 左右导数符号不同,则取极值。
5. 判别极值的第二充分条件
设 f(x) 在 x = x_0 处二阶可导,且 f'(x_0) = 0 , f''(x_0) \neq 0 。
- 若 f''(x_0) < 0 ,则 f(x) 在 x_0 处取极大值。
- 若 f''(x_0) > 0 ,则 f(x) 在 x_0 处取极小值。
6. 判别极值的第三充分条件
设 f(x) 在 x = x_0 处 n 阶可导, f^{(m)}(x_0) = 0 , f^{(n)}(x_0) \neq 0 ( m = 1, 2, \dots, n-1 , n \geq 2 )。
- 当 n 为偶数且 f^{(n)}(x_0) < 0 时,取极大值。
- 当 n 为偶数且 f^{(n)}(x_0) > 0 时,取极小值。
- 当 n 为奇数时,不是极值点。
7. 凹凸性的定义
定义1 :
f(x) 在区间 I 上连续,对于 I 上任意两点 x_1, x_2 ,恒有:
f\left(\frac{x_1 + x_2}{2}\right) < \frac{f(x_1) + f(x_2)}{2}
则称 y = f(x) 在 I 上的图形是凹的。
f(x) 在区间 I 上连续,对于 I 上任意两点 x_1, x_2 ,恒有:
f\left(\frac{x_1 + x_2}{2}\right) > \frac{f(x_1) + f(x_2)}{2}
则称 y = f(x) 在 I 上的图形是凸的。
可以更一般地写为:
f(\lambda_1 x_1 + \lambda_2 x_2) < \lambda_1 f(x_1) + \lambda_2 f(x_2),
其中 \lambda_1, \lambda_2 \in (0, 1) , \lambda_1 + \lambda_2 = 1 。
定义 2:
f(x) 在 [a, b] 上连续,在 (a, b) 上可导,在(a,b)内任意 x 及 x_0 ( x \neq x_0 )均有:
f(x_0) + f'(x_0)(x - x_0) < f(x) 则称f(x)为凹函数;
f(x_0) + f'(x_0)(x - x_0) > f(x) 则称f(x)为凸函数
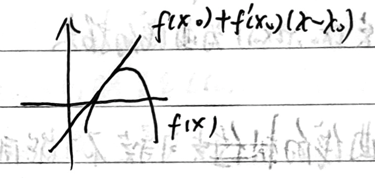
8. 拐点定义
连续曲线的凹与凸的分界点称为该曲线的拐点(是一个点,不是值(x_{0},f(x_{0}))。对比:极值点是横坐标)
9. 凹凸性的判别
f(x) 在 I 上二阶可导。
- f''(x) > 0 ,则 f(x) 在 I 上是凹的。
- f''(x) < 0 ,则 f(x) 在 I 上是凸的。
10. 二阶导是拐点的必要条件
设 f''(x_0) 存在,且 (x_0, f(x_0)) 为拐点,则 f''(x_0) = 0 。
拐点不要求二阶导存在。(如 y = \sqrt[3]{x} , x = 0 处)
11.判别拐点的第一充分条件
f(x) 在 x = x_0 处连续。\overset{\circ }{u} (x_0,s)二阶导数存在,
该点左右邻域内f^{\prime}(x)变号,则点(x_0,f(x_0))为曲线的拐点.
12.判别拐点的第二充分条件
f(x) 在 x = x_0 的某邻域内三阶可导,且 f''(x_0) = 0,f'''(x_0) \neq 0,则 (x_0, f(x_0)) 为拐点。
13.判别拐点的第三充分条件
f(x) 在 x_0 处 n 阶可导,且 f^{(m)}(x_0) = 0 (m = 2, \dots, n-1),f^{(n)}(x_0) \neq 0,且 n 为奇数,则 (x_0, f(x_0)) 为曲线的拐点。
14.曲线的极值点与拐点的关系
曲线的可导点不可能同时为拐点和不可导点。
曲线的不可导点可能同时为拐点和不可导点。
15渐近线
1. 铅直渐近线
- 若 \lim_{x \to x_0^{+}} f(x) = \infty 或 \lim_{x \to x_0^-} f(x) = \infty,则 x = x_0 为一条铅直渐近线。
2. 水平渐近线
- 若 \lim_{x \to \infty} f(x) = A,则 y = A 为水平渐近线。
3. 斜渐近线
- 若 \lim_{x \to \infty} \frac{f(x)}{x} = a,\lim_{x \to \infty} [f(x) - ax] = b,则 y = ax + b 是一条斜渐近线。
16.曲率与曲率半径
- 曲率 K = \frac{|y''|}{(1 + (y')^2)^{\frac{3}{2}}}
- 曲率半径 R = \frac{1}{K}